あやとりトピックス 251-260
「名前なし」 2025/02/14
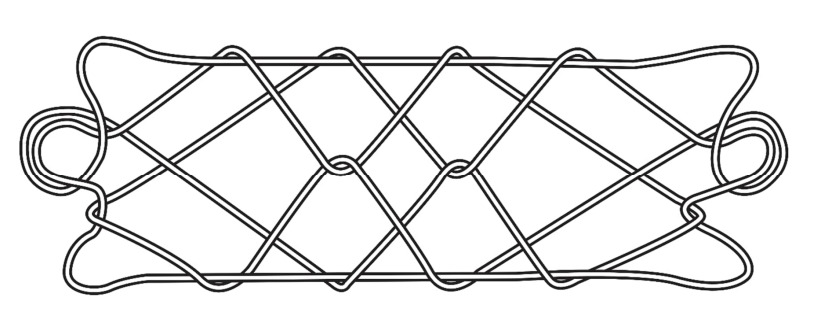
C. F. Jayne 氏の「String Figures and How to Make Them」 に「名前なし(No Name)」というあやとりが載っています。これは、W. H. Furness 博士(Jayne 女史の兄)がカロリン諸島のナティク島で、エミリという女性から採集したものです。Jayne 氏はそれを知る前に「ブロスバードの家」を元にこのあやとりを創作していました。そのため「名前なし」として発表しました。
cited from "String Figures and How to Make Them"
その後、このあやとりはオセアニアで広く採集されました。
ソシエテ諸島の「壊れた(Broken)」
ツバルの「2つの村(Two Villages)」
オーストラリアの「2頭のカンガルー(Two Kangaroos)」
ギルバート諸島の「敗者の戦い(Fight of the vanquished)」
ソロモン諸島の「おおこうもり(Flying fox)」
パプアニューギニアの「橋が壊れる(Breaking a Bridge)」
などです。
これと同じできあがりで取り方の全く異なるあやとりがアフリカで採集されています。
タンザニアの「穴(Pit)」
モザンビークの「国境(Border Between Two Countries)」
各地での見立てが見事にばらばらで興味深いです。わたしなど、どう考えてもこれがカンガルーには見えません。
さて、これらのあやとりはできあがりの形から、日本では「2匹の魚」などと紹介されていることがあります。しかし、このあやとりが魚をモチーフにしているという記述は見当たりません。これだけ広範囲に採集されているのに、魚に見立てた地域がまったくないというのも面白いですね。これが魚に見えるのは日本人だけなのでしょうか。
この形を魚に見立てた創作あやとりもあります。有木昭久氏の「金魚」、神谷和男氏の「2匹の魚」 などです。ちなみに、野口先生の「あやとり続 」に「落とし穴」というあやとりが載っています。取り方は「名前なし」のものです。名前がないので「穴」を拝借したそうです。同じあやとりと書いてありますが、同じではありません。
k16@ISFA
「返し取り」用語の初出文献調査 2025/02/10
国内外のあやとり教本には、教本の前付け部分に「人差し指の構え」や「中指の構え」(名称は教本によって異なります)といった基本の取り方の説明が掲載されているのをよく見かけます。
こうした基本の取り方の一つに「返し取り」という取り方があります。これは上記「人差し指の構え」もしくは「中指の構え」の状態で、親指以外の指を親指の輪の中に入れて、親指以外の指で親指手前の紐を取って親指の紐を外す、という取り方になります。
過去のトピックを振り返ると、2002年に投稿されたトピック 037 に「返し取り」の用語が既に登場しています。
しかしながら、この「返し取り」という用語はいつ頃から使われるようになったのか、つまり初出はどの文献なのかは不明のままでした。
また「返し取り」の用語に対応する英語表記は、海外のあやとり関連文献には見当たりません。
そこで日本で過去に出版されたあやとり教本を対象に、「返し取り」用語の初出文献調査を行いました。
2025年2月1日時点において、日本でこれまで出版されたあやとり教本(折り紙などあやとり以外のものが一緒に掲載されていない教本に限る)は241冊あると推定されます(独自調査)。そのうち絶版等で入手困難なものを除いた、保有している220冊(出版年代が1973年から2025年1月までのもの)を対象に、教本前付け部分にて「返し取り」の用語が記載されているかどうかを調べました。
その結果、前付け部分に「返し取り」の用語が紹介されていた数は14冊で、その中で最も古く出版された教本は、1982年出版の『あやとり いととり2
そこで1982年以前に出版された他のあやとり教本において、本文などの前付け部分以外に「返し取り」の用語が記載されているか追加調査しましたが、該当する教本は見当たりませんでした。
従って、日本で過去出版されたあやとり教本の約9割にあたる220冊を対象とした調査結果であることに留意は必要ですが、「返し取り」の用語が初めて登場した文献はおそらく上記1982年出版の教本『あやとり いととり2』だと思われることが分かりました。
ちなみに、上記『あやとり いととり2』以外で「返し取り」が前付けで紹介されていた教本は、斎藤たま氏とは別の様々な著者や監修者によるものでした。また、他の基本の取り方についても教本前付けでの紹介冊数を調べたところ、「中指の構え(166冊)」「人差し指の構え(151冊)」「始めの構え(91冊)」「ナバホ取り(64冊)」「ナバホの構え(19冊)」で、「返し取り(14冊)」がそれに次ぐ数であったのは興味深い結果でした。
上記斎藤たま氏の教本『あやとり いととり2』ですが、斎藤たま氏が著者としてこれまで日本で出版されたあやとり教本は、この『あやとり いととりシリーズ』のみとなっています。
その斎藤たま氏が1970年頃から約30年かけ、日本全国を旅して日本の民俗文化を調査・記録した民俗調査カードが東京文化財研究所に保管されており、現在データベース化(サイトはこちら )されています(詳細はトピック 229 をご参照ください)。
この民俗調査カードのうち、あやとりに関する記録をまとめた内容が、国際あやとり協会の会誌「BISFA Vol.11 , 日本語版 」として出版されており、『あやとり いととりシリーズ』の教本は斎藤たま氏の民俗調査記録の一部をもとに執筆されていたことが、その「BISFA Vol.11」(英語版・日本語版の6ページ)に記載されています。
そこであやとりに関して記録された民俗調査カード(約二千枚)の中から「返し取り」用語の記録があるかを調べたところ、「返し取り」の取り方に対応する記録として「かえし(例:カードID 54733 )」や「かえしどり(例:カードID 54739 )」という文言での記録が複数確認されただけでなく、「ひっくり返す(例:カードID 53297 )」という文言で記録されているものも複数あったことが分かりました。
また教本『あやとり いととり2』に掲載されている作品のうち、「返し取り」の工程を行う作品が記録された調査カードを確認すると、「返し取り」に対応する記録箇所は全て「ひっくり返す」という文言で記載されていたことも判明しました。
ただ教本『あやとり いととり2』では、返し取りを行う作品であっても工程数の少ない作品であれば、「かえしどり(返し取り)」の用語は使用されずに返し取り一つ一つの工程が紙面上で説明されている一方で、工程数が多い作品の場合、「かえしどり(返し取り)」の用語が使用され、返し取り一つ一つの工程の説明は省略されています。
従ってここからは推測ですが、返し取りを行う工程数の多い作品を教本に掲載する際、紙面の都合で掲載工程数を省略するために、調査カードでは「ひっくり返す」という文言で記録していた一連の工程に対し、「かえしどり(返し取り)」という用語を造語し教本で用いたのではないかと考えられます。そして民俗調査カードに「かえし」や「かえしどり」の用語が記録されたのは、それらの調査カードの記録年代や追記したと思われる筆跡の違いから推測するに、その造語以降だと考えられます。
結論として、初めて「返し取り」の用語が用いられたのは1982年出版のあやとり教本『あやとり いととり2』(福音館書店 さいとうたま 採取・文 / つじむらますろう 絵)だと思われ、「返し取り」の用語は紙面の都合により造語され用いられたのではと考えられます。
他の一連の工程の呼び名、例えば「ナバホ取り(Navajo、Navaho Movement)」といった用語は海外の文献発祥のため英語表記がありますが、この「返し取り」の用語は国内発祥と思われ英語表記はまだないことから、今後この「返し取り」の用語がより一般的な表現となり、海を越えて英語表記が新たに誕生しても不思議ではないでしょう。
(※当トピックの内容について、福音館書店様より当協会ホームページへの掲載許諾を頂いております。また「返し取り」の造語経緯の考察は福音館書店様が保証するものではないことご留意ください。)
加藤直樹@ISFA
「ちびと山賊の家 あやとりを楽しむ会」報告~野口ともさんをお迎えして~ 2024/12/13
2024年12月7日(土曜日)埼玉県のとある家庭のイベント広場「ちびと山賊の家」であやとりを楽しむ会が開かれた。
集まったのは34名、前半、野口とも先生に野口廣先生があやとりを始められた経緯、あやとり協会の立ち上げ、パプアニューギニアへのあやとり採集のお話、国際あやとり協会の本部がアメリカに移るまでの経緯など、お聞きした。
更に野口廣先生を中心にしたあやとりの活動、日本でのあやとりの本の相次ぐ出版、マスコミでの広がり、あやとりコンテストの開催のお話、皆さん、熱心に聞き入りあやとりが世界的に貴重な文化であること、その面白さ、奥深さを知る良い機会になった。
次に野口とも先生のご指名と解説により、世界のあやとりがお客様に披露された。実は集まった人の中には「あやとり初級マスター」、「あやとり中級マスター」、「あやとり上級マスター」、「あやとりグランドマスター」等あやとり教室指導員、合わせて10人近くが揃っていて、お客様に世界のあやとりをその場で披露することができたのだ。
集まった人たちは世界中のあやとり、珍しいあやとり、難解なあやとり、本に掲載されている美しいあやとりなど、一度にたくさん見ることができ、早わざ、難解技に目をぱちくり、拍手喝采、あやとりの素晴らしさに感動した。
九つのダイヤ
耳の大きな犬
テントの幕
火山
小舟→かに
つがいのライチョウ
披露されたあやとりは25種類、次の通り。日本のあやとり 「ぱんぱんほうき」「富士山」「流れ星」、アフリカのあやとり 「バトカ峡谷」「草ぶきの家」、アメリカ、ナバホのあやとり 「たくさんの星」「ナバホの蝶」「テントの幕」、ハワイのあやとり 「九つのダイヤ」、南米のあやとり 「コウモリの群れ」「火山」、オセアニアのあやとり 「小舟→カニ」「真昼の太陽」「アムワンギョ」「天の川」「ワニ」、極北圏のあやとり 「山間の日の出」「つがいのライチョウ」「耳の大きな犬」「ダンスハウスで踊る人々」「柳の中のトナカイ」「そりを引くトナカイ」。折しもクリスマス、3人でとるクリスマスツリーに星が灯った「クリスマスツリー」、そして「お星さま」。
クリスマスツリーとお星さま
その後、指導員やあやとりマスターのところに自由に集まって、やりたいあやとりを行った。幾つもの輪ができて一時間、皆全集中で、あやとりに取り組んだ。教わる人、教える人、熱気むんむんで一時間はあっという間に過ぎた。
優しいあやとりが幾つかできるようになった人、難しいあやとりを何とかクリアーできた人、あと一歩というところで、あとは本を見てという人、みんな「楽しかった!」「満足です!」「お話も面白かった!」「またやってください」との声多数。
係からは「大成功ですね!」の喜びの声、会の最後に参加者全員であやとりの星を作り、記念の集合写真を撮った。
全員で「お星さま」
後日、参加者から以下の感想文が寄せられた。
先日はあやとりを楽しむ会の講演、イベントに参加させていただき本当にありがとうございました。
とも先生のお話で知らなかったあやとりの奥深い素晴らしい世界を知ることができました。
大先輩指導員の方とご一緒させて頂いたり、直接指導もして頂きたくさんの学びと喜びを感じる機会となりました。
そしてたくさんの方にあやとりの楽しさ、喜びを伝えることができ嬉しかったです。
私も学びを続けていきたいと思います。
報告書の原稿提供:廣田弘子 & 写真提供:沼田薫、嶋津香 & 編集:野口とも@ISFA
第34回野口廣記念あやとり講習会・検定報告 2024/11/27
秋晴れの2024年11月16日(土)に東京代々木の国立オリンピック記念青少年総合センターで第34回野口廣記念あやとり講習会・検定が開催されました。
大変残念なことにこの日は最寄り駅の新宿駅で電車の事故があり、多くの方が不参加となってしまいました。けれども、講習会の指導員は予定通り10数名の方が無事に参加されたので講習会や検定には差し支えありませんでした。
講習会ではいつも通り、指導員の方たちの実演によって今日指導するあやとりの紹介がありました。指導には前回に「あやとり教室指導員」の資格を取得した方々も指導に当たられたので、初級から上級まで26種類ものあやとりが取り上げられました。その中のいくつかを紹介します。
ぱんぱんほうき
テリハボクの花
いなずま
小舟→かに
白鳥
三つの星
キツネとクジラ
参加者の方々は160人部屋にゆったりと座って、それぞれ覚えたいあやとりの先生の所で思う存分新しいあやとりに取り組み、沢山のあやとりをマスターされて大変楽しく満足のいく会になったと思います。
今回よりあやとり検定ではスタンプカードを導入しました。検定で合格する度にそのあやとり名の横に「合格」のスタンプが押されます。初級全部に合格が押されたら「初級あやとりマスター」の称号と賞状が与えられます。中級全部に合格したら「中級あやとりマスター」の称号と賞状が与えられます。上級全部に合格したら「上級あやとりマスター」の称号と賞状が与えられます。
初級、中級、上級すべてに合格したら「あやとりグランドマスター」の称号と賞状、及び記念のバッジが与えられます。
このほかに、初級2回中級3回上級5回に合格したら「あやとり教室指導員」の資格を取得することができます。
今回も受験者は全員が合格して、たくさんの合格証や「あやとり教室指導員」の賞状を取得してお帰りになりました。
次回の開催は2025年3月29日(土)を予定しております。
2024年暮れから国際あやとり協会のホームページでお知らせを公表します。
参加申し込みは2025年2月1日~28日の間にホームページより受け付けますので皆さんふるってのご参加をお待ちしています。
報告:野口廣記念あやとり講習会・検定 世話人 野口とも@ISFA & 写真提供:青木幸久、嶋津香
港区立伝統文化交流館で昔遊び その3 2024/10/30
2024年10月26日(土)12時〜16時に港区立伝統文化交流館にて、「ものづくりフェア」の一環として昔遊びの会を行いました。(同会場での過去のイベントの様子はこちら とこちら をご覧ください)
この昔遊びの会には「たま川お手玉の会」と「国際あやとり協会」が指導側として参加し、
季節の折り紙を飾った色紙を作る
指編みであやとり紐を作り、出来上がったあやとり紐であやとりをとる
の二つのイベントが行われました。
当協会会員を含む指導者は上記2のイベントに参加し、あやとりを刺繍したタペストリーも飾りました。
参加者の皆さんはとても楽しんでくださいました。下記の写真をご覧ください。参加された皆さんの熱気が伝わってきますね。
当日港区立伝統文化交流館にご来場くださった皆様、スタッフの方々、本当にありがとうございました。
指導した人:伊藤ひで、吉井よし子、山野憲子、服部知明、青木萬里子、青木幸久(写真係)、福田恵美、栗田亮佑
吉田仁子@ISFA
「第1回あやとりと楽器のコンサート」イベント報告 2024/09/20
2024年6月30日、宮崎県の「みやざきアートセンター」で「第1回あやとりと楽器のコンサート」が開催されました。
みやざきアートセンターはあやとり彫像のある会場です(詳しくはこちら )。
このコンサートは、楽器演奏とあやとりパフォーマンスを組み合わせたユニークなイベントで、ISFA会員の成松高嗣君が設立したTEAM AYATORIによるあやとりパフォーマンスが行われました(TEAM AYATORIに関するトピックはこちら )。
テーマは「動物」で、演奏も子どもたちが中心となり、動物に関するいろんな音楽に合わせて、「耳の大きな犬」「たたかうライオン」「白鳥」など、さまざまなあやとりが披露されました。
とても大盛況だったようで、今年度で全3回の開催が企画されているようです。
イベント時の様子の詳しい内容については、TEAM AYATORI公式サイト をご覧ください。
加藤直樹@ISFA
異文化間におけるあやとりの類似性解析に関する研究論文の紹介 2024/08/23
「A global crosscultural analysis of string figures reveals evidence of deep transmission and innovation 」(Roope Oskari Kaaronen, Matthew J. Walsh, Allison K. Henrich, Isobel Wisher, Elena Miu, Mikael A. Manninen, Jussi T. Eronen, and Felix Riede : 2024) というあやとりに関する研究論文が、2024年の1月にWeb上で公開されました。(補足資料を含めると約80ページの論文)
またYoutubeにて、論文筆頭著者のRoope Oskari Kaaronen氏による、この研究内容に関する講演動画 が今年6月に公開されました。
Kaaronen氏はISFA会員で、フィンランドにあるヘルシンキ大学の博士研究員です。
Kaaronen氏の研究対象は、認知科学、(認知)人類学、文化の進化、複雑性科学、持続可能性科学であり、過去と現在、異文化間の境界を越えて、テクノロジーや文化がどのように進化していったかに興味があるとのことです。(ヘルシンキ大学のKaaronen氏紹介ページ や氏の個人サイト より)
あやとりは、世界中の文化の境界を越えて最も普及している遊びの一つであり、数学的に記述することが可能であることから、文化の伝達を研究するための優れた媒体である、とKaaronen氏は講演で述べています。
この度Kaaronen氏に確認し、論文紹介の許諾をいただきました。以下拙訳で恐縮ですが、論文の内容を紹介したいと思います(講演の内容も一部参考にしています)。
論文紹介の都合上、実際の論文とは異なる構成で紹介していますこと、ご了承ください。(この論文は、「プレプリントサーバー」という、査読の過程を経ないで素早く論文をネットに公開できる環境で公開されているため、データや方法の質、結果の信頼性などには注意を払う必要があります)
【どんな研究論文?】
あやとりの類似性を調べる数学的な変換手法を考案した
世界中の92の異なる文化圏で記録された826のあやとり作品を対象に、作品の類似性に関する解析を行った
近隣の文化地域内では、類似するあやとり作品がより見つかる可能性が高い結果が得られ、これまで直感的に観察していたことを世界規模のデータセットで実証した
【過去の研究と比較して、この研究のすごいところは何?】
過去に提案された、あやとり作品を数字や記号の情報に変換する手法は、他の作品と類似性を比較できる手法ではない
この研究では、2本の紐が交差している箇所に着目し、あやとり作品の類似性を比較することが可能な変換手法を考案した
【研究結果は?】
826のあやとり作品を解析して類似性を調べた結果、異文化間で同一する作品として、380作品を83の同一作品に分類することができた
近隣の異文化地域では、類似するあやとり作品がより見つかる確率が高い
異文化間で同一する作品のうち幾つかは、位置も全く異なる世界中の様々な文化地域で見られる作品もあった
【データ、方法、結果の整合性において留意すべき点はある?】
インターネットによって文化伝達の性質が根本的に変化したと推測されるため、原則として1990年以前に記録されたあやとり作品を調査対象とした
研究実施の制約上、各文化地域から最大25の数のあやとり作品を調査対象とした(最大25作品数の国・地域は、日本、カッパー・イヌイット、ティコピア、ユピクなど)
2本の紐が明らかに交差している状態のみ数学的な変換ができるため、数学的な変換が可能でないあやとり作品もあり、全てのあやとり作品に適用した手法ではない
作品が描かれたイラストから数学的な変換を行っているため、イラストが不正確に描かれていたり、紐を引っ張る力によって完成形の形状が大きく変わる場合、作品の類似性の結果に影響を与える
【得た結果に対して議論すべき点はある?】
近隣の文化地域内では、類似するあやとり作品がより見つかる確率が高いという結果は、距離の近さが文化の伝達における重要な要素である考えを裏付けている
4段ばしごの作品は世界中の様々な文化地域でみられる結果であったが、作り方が多くの異文化地域で一致していたり、比較的複雑な作品であることなどから、4段ばしごの起源はもっと昔まで遡った共通の起源がある可能性を示唆している
【今後の課題は?】
調査対象であるあやとり作品数を増やす
個々の文化地域に対象を絞って局所的に類似性を調べる
以下、あやとり作品の数学的な変換手法と、類似性の調査方法をメインに、論文の内容について詳しく解説したいと思います。
〈あやとり作品の数学的な変換手法について〉
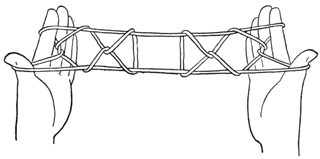
論文では、「String Figure Bibliography」に記載のいくつかの資料から、世界中の92の異なる文化圏で記録された826のあやとり作品を解析対象としています。類似性の解析を行うために、あやとり作品を“数字の並び”に変換する必要があり、あやとり作品の完成形のイラストから以下のステップに従って変換を行っています。(論文では、下図の4段ばしごの作品を例に変換手順について説明しています)
適当な場所(下図の左上の黒丸)から、時計回り・反時計回りのどちらか一方向に紐をたどる(下図では時計回り)
2本の紐の交差に当たったら、交差する箇所に数字を順に割り当てていく(既に割り当てた交差を再度通っても、数字は再度割り当てない)
全ての交差に数字を割り当てたら、再度黒丸の箇所から紐をたどっていき、交差に当たったら割り当てた数字を列記していく。このとき、交差する紐の上を通ったら正の数、紐の下を通ったら負の数とする
スタート位置(黒丸)に戻るまで数字を列記していく
4段ばしご作品の“数学の並び”への変換作業の図(論文の図7)
4段ばしごの例では、列記した“数字の並び”は以下のようになります。
-1, 2, -3, 4, 5, -6, 7, -8, -9, 10, -11, -12, 13, 14, -15, 16, -17, 18, -4, 3, 19, -20, -2, 1, 21, -22, 23, 24, -25, -26, 27, 17, -16, -13, 12, 11, -10, 9, 8, -7, -14, 15, 6, -5, -18, -27, 26, -19, 20, 25, -24, -23, 22, -21
この方法は「Gauss code」や「Gauss notation」と呼ばれ、結び目理論の分野で用いられる手法の一つになります。このGauss codeの手法によって作品を数字に変換することができ、人間の目による感覚で判断するのではなく、変換した“数字の並び”によってあやとりの類似性を調査する試みをこの研究では行なっています。
しかしながら、4段ばしごの作品をGauss codeの手法により数字に変換した時、必ずしも上記の数字の並び方だけになるとは限りません。なぜならスタートの黒丸の地点が色々考えられたり、紐をたどる方向も時計回りと反時計回りの2パターンあることや、作品を手前側から見るか向こう側から見るかによっても数字の並び方が変わってくるためです。そのため、そうした“数字の並び”の様々な条件を全て網羅し列記したもの(ここでは便宜的に“網羅した数字の並び”と呼びます)に変換する新たな手法が考案され、類似性の調査を可能にしました。詳細について興味のある方は論文をご覧ください。
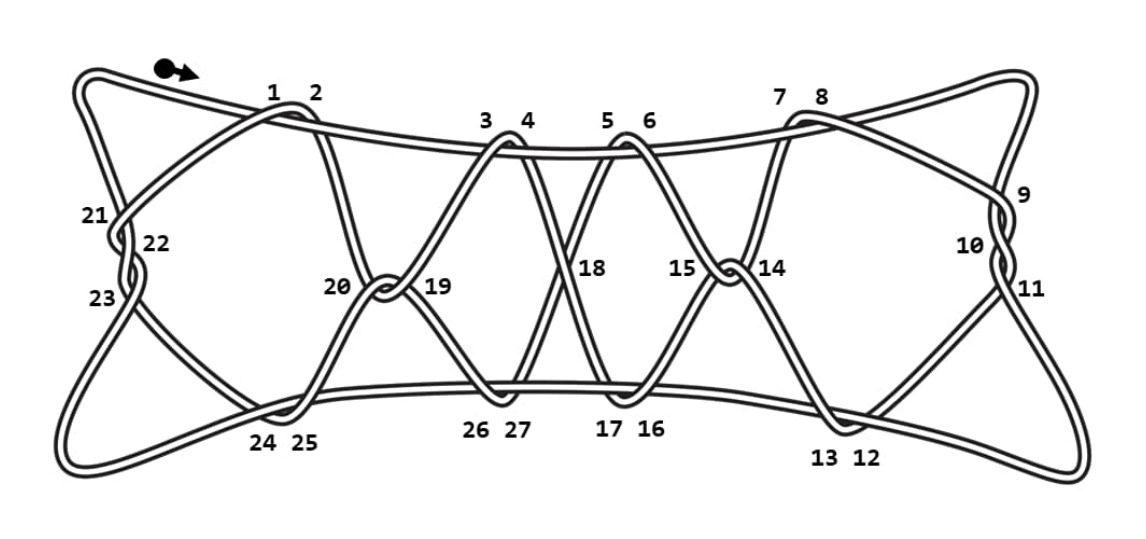
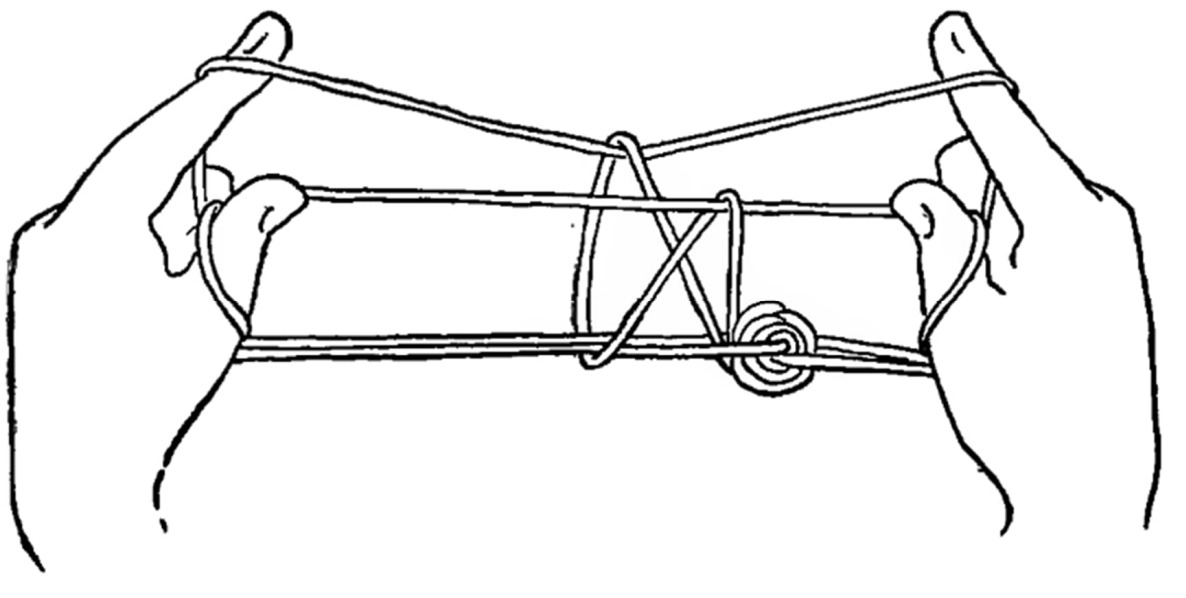
しかし、例えば下図の「ナバホの蝶」の作品の中央下部では紐が多重に巻き付いており、そこでは複雑な紐の交差を持つため、このGauss codeの手法を用いて“数字の並び”に変換することができません。そのため、全てのあやとり作品に適用可能な手法ではないことが論文では触れられています。
「ナバホの蝶」作品のイラスト(論文の図S5)
ちなみにこの“網羅した数字の並び”が記載されたデータは、あやとり作品の複雑さの直感的な推定にも使用することができる、と述べられています。
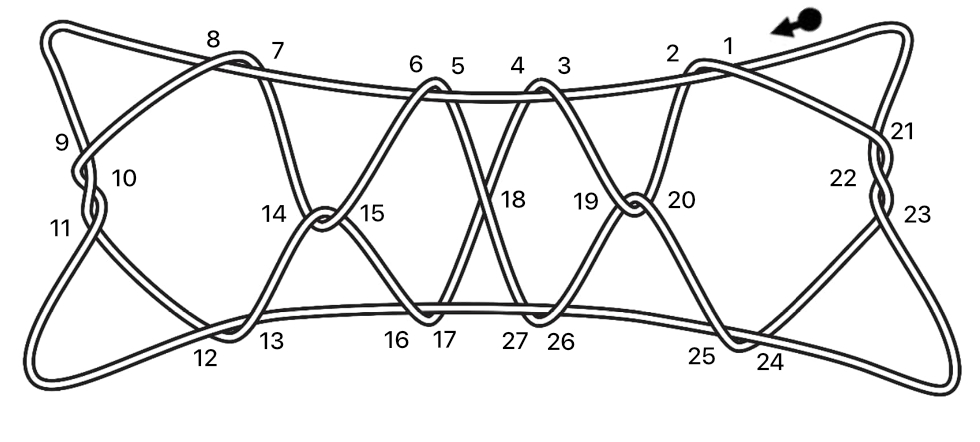
また作品に対称性があると、非対称性の作品と比べて、“網羅した数字の並び”の中に重複した数字の並びがより多く出現します。例えば下図の4段ばしごの例では、上記の4段ばしごの“数学の並び”への変換時とは、スタート地点と紐をたどる方向が異なりますが、変換した“数字の並び”同士を比較すると、18の交差部分(下記“数学の並び”の太字箇所)を除いて一致していることが分かります。
4段ばしご作品の“数学の並び”への変換作業の図(論文の図7とは異なるスタート地点・紐をたどる方向で新たに作成)
-1, 2, -3, 4, 5, -6, 7, -8, -9, 10, -11, -12, 13, 14, -15, 16, -17, -18 , -4, 3, 19, -20, -2, 1, 21, -22, 23, 24, -25, -26, 27, 17, -16, -13, 12, 11, -10, 9, 8, -7, -14, 15, 6, -5, 18 , -27, 26, -19, 20, 25, -24, -23, 22, -21
理想的にはあやとり作品の複雑度は、その作品の構造をできるだけ簡潔に記述するためのコンピュータプログラムの最短長さの尺度で測定できる、とあり、そうした尺度ではデータ内に重複したものがあると「再度繰り返す」といった言葉で簡潔に記述することになります。
この論文ではそうした複雑度の概算として、簡易的にZIPのDEFLATEアルゴリズムを用いることで、対称性のある作品の“網羅した数字の並び”内の重複データは圧縮され、ZIPにより圧縮されたファイルサイズ(kB)を複雑度の推定値として使用しています。
〈あやとり作品の類似性の解析手法について〉
とある二つの“あやとり作品”の類似性を調べることは、上述した数学的変換を行うことで得られる、二つの“網羅した数字の並び”がどれだけ似ているかを調べることに対応します。こうした“網羅した数字の並び”の類似性を調べる方法として、論文では「q-gram」(q-gramsやn-gramとも呼ばれます)と「コサイン距離(cosine distance)」の手法を用いています。これらは、自然言語学分野において、文字列がどの程度似ているかを調べる手法として知られています。
論文には、「q-gram」「コサイン距離」を用いたあやとり作品の類似性解析に関する詳細の解説がありません。ただ、あやとり作品の“網羅した数字の並び”への変換や、q-gramを用いたコサイン距離の算出は、Rというプログラミング言語を用いて行われており、この論文が公開されたサーバー上に、解析データやプログラミングコードも一緒に公開されています。そのコードを見ると、Rのstringdistパッケージ(文字列の類似性を調べる関数群をまとめたもの)を用いて、q-gramによるコサイン距離の算出がされていることが確認できます。そのため、このstringdistパッケージについて説明している資料を参考に、以下、論文にはない例を挙げて、「q-gram」「コサイン距離」を用いた類似性解析の説明をします。
例えば、あやとり作品AとBをそれぞれ“網羅した数字の並び”に変換し、以下のようになったとします。(あくまで例のため、“網羅した数字の並び”自体は正確でなはく適当です)
「q-gram」とは、q個の数で文字列を分割していく手法のことで、例えば
q=2
とすると、
作品B:
{
1 ,
2 }
{
2 ,
3 }
{
3 ,
4 }
のようになります。
そして「コサイン距離」とは、二つのベクトルの向きがどの程度近いかによって、比較対象がどのくらい似ているかを調べる指標で、ベクトル
a
=
(
a 1 ,
a 2 ,
…
,
a n )
、
b
=
(
b 1 ,
b 2 ,
…
,
b n )
のコサイン距離は以下の式により求めることができます。
1
−
cos
(
a
,
b
)
=
1
−
a
⋅
b
∥
a
∥
∥
b
∥
=
1
−
∑
i
=
1
n
a
i
b
i
∑
i
=
1
n
a
i
2
∑
i
=
1
n
b
i
2
文字列の類似性解析においては、二つのベクトルの向きが近いほど(つまり二つのあやとり作品が似ているほど)0の値に近づき、向きが異なるほど(二つの作品が似ていないほど)1の値に近づきます。
コサイン距離を求めるためには、作品AとBをそれぞれベクトルに変換する必要があります。
例で挙げた作品AとBにおいて、q=2のq-gramで分割した組み合わせを全て記載すると、{
1 ,
2 }
{
2 ,
3 }
{
3 ,
4 }
例えば作品Aでは、上記3つの組み合わせのうち、左から1番目と2番目
{
1 ,
2 }
{
2 ,
3 }
{
3 ,
4 }
a
=
(
1
,
1
,
0
)
となります。同様に作品Bを考えると、左から1番目、2番目、3番目の全てを1つずつ持っているので、作品Bのベクトルは
b
=
(
1
,
1
,
1
)
となります。
これら二つのベクトルを用いて、上の式によりコサイン距離を計算すると、作品AとBの例では、コサイン距離は約0.18と求められます。
もし、比較するあやとり作品の数字の並びがともに
1 ,
2 ,
3 ,
4
だとすると、ベクトルはともに
a
=
b
=
(
1
,
1
,
1
)
となり、コサイン距離を算出すると0になります。これは同一作品という結果であり、ともにベクトルの向きが一致しています。また、比較作品の“網羅した数字の並び”がそれぞれ
1 ,
2 ,
3
と
4 ,
5
だとすると、ベクトルはそれぞれ
a
=
(
1
,
1
,
0
)
、
b
=
(
0
,
0
,
1
)
となり、コサイン距離は1になります。これは非同一作品という結果であり、ベクトルの向きは90°となって全く同じ方向を向いていません。
上記の例は3次元のベクトルでしたが、論文では“網羅した数字の並び”の数字の数はもっと沢山あるため、多次元ベクトルで考えることになります。そうした多次元でも上の式に当てはめてコサイン距離を求めることができ、このコサイン距離によって、あやとり作品から変換した“網羅した数字の並び”を解析して類似性を調べることができます。
ここまで、類似性の解析手法を説明するため論文にはない例を挙げました。
実際の論文のq-gramの解析ではq=3が使用されています。これは3つの連続する交差が最小の関心構造であるからだと論文では述べられています。
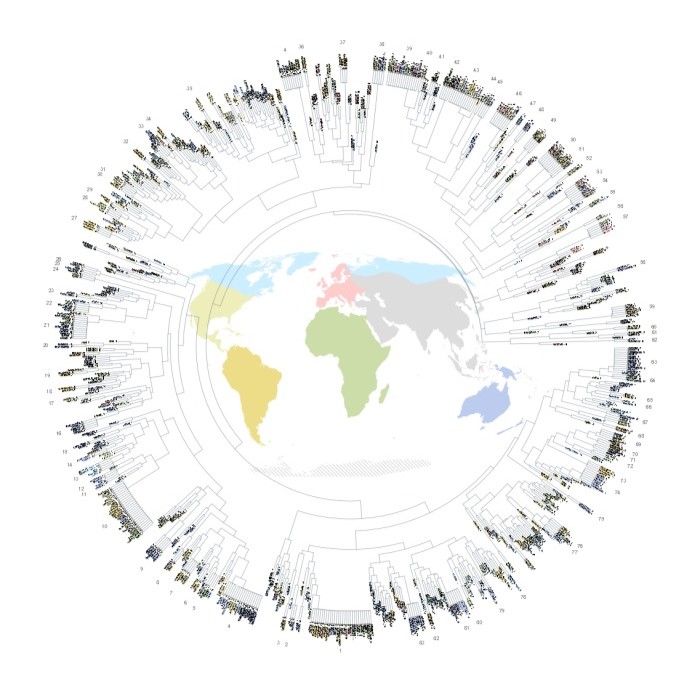
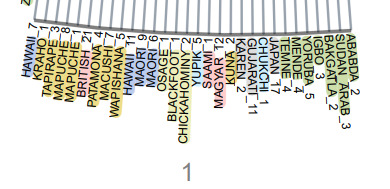
この算出したコサイン距離の値に基づいて、クラスター分析の最長距離法(最遠隣法や完全連結法とも呼ばれる)という手法を用いて、世界中の92の異なる文化圏で記録された826作品をグループ分けし、下図のようなツリー構造が図示されています。ただ図のサイズが大き過ぎるため、拡大して見たい場合はこの図のファイルが格納されているこちら をご覧ください。
クラスター分析による樹形図(論文の図3)
この826作品のうち580作品が、異文化間でほぼ同一の作品として83のグループに分類されており、ツリー構造の最下部(最も似ている作品群)に下から 1, 2, 3, …, 83 と番号が振られています。グループ分けされた83の作品群の詳細は、論文のSupplementaryの表1に記載されています。
ここで、もし比較する二つの作品が全く同じイラストで描かれていたなら、それらのコサイン距離は0になるはずです。しかし、イラストの交差部分が不正確に描かれていたり(交差部分で交わる紐の上下の位置が逆になっているなど)、紐を引っ張る力によって完成形の形状(交差の数や並び)が大きく変わって、同じ作品であってもコサイン距離が0にならない、といったことが解析上起こりました。その結果、ツリー構造の最下部(最も似ている作品群)にある各83グループ間での作品の類似性の解析ではコサイン距離は完全に0にはならず、0から0.1程度の値になっています(この結果はプログラミングコードを実行することで得られます)。そのため類似性解析の結果、コサイン距離が0.1未満だった作品群を同一作品とみなしているそうです(0.1を閾値に設定した明確な根拠が論文には記載されていなかったので、直接Kaaronen氏に確認しました)。
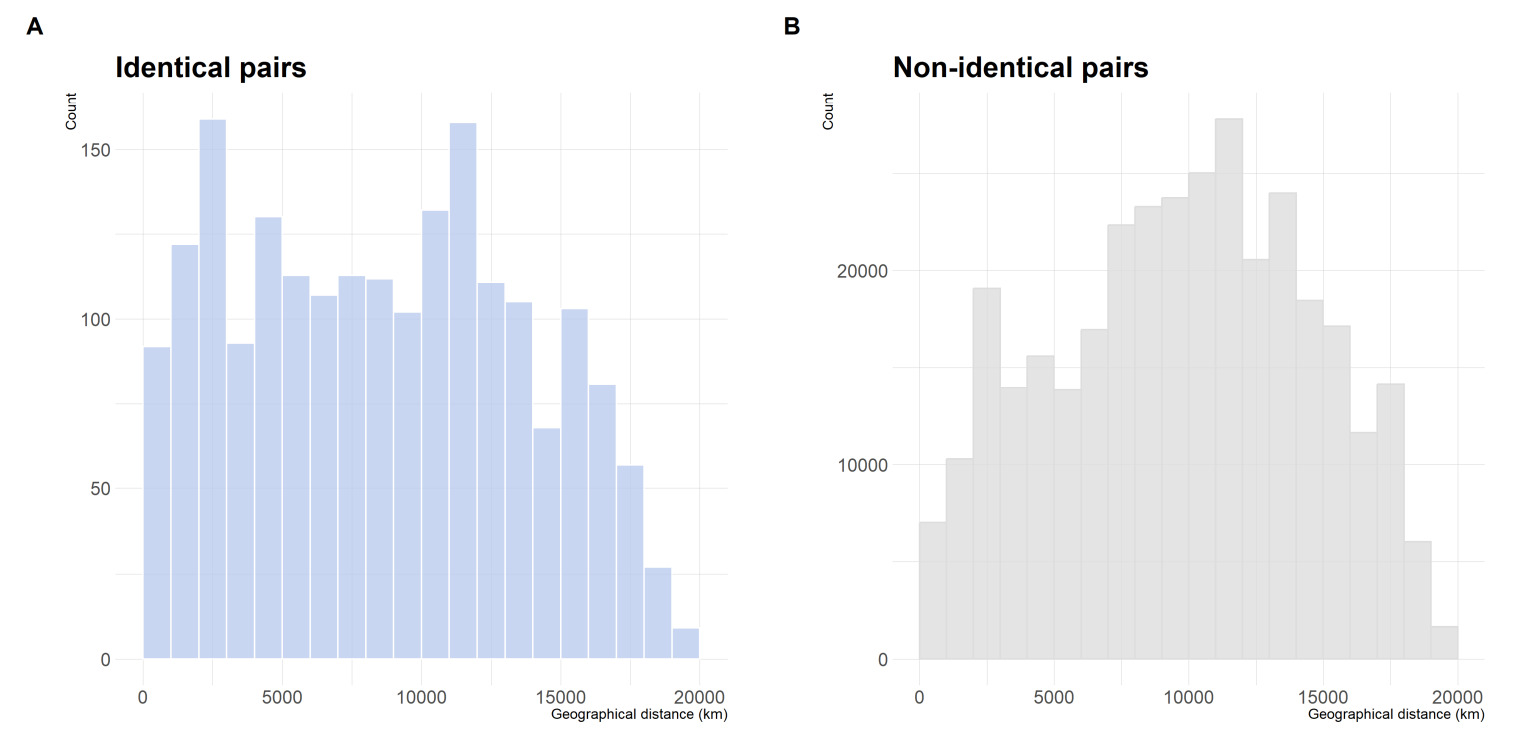
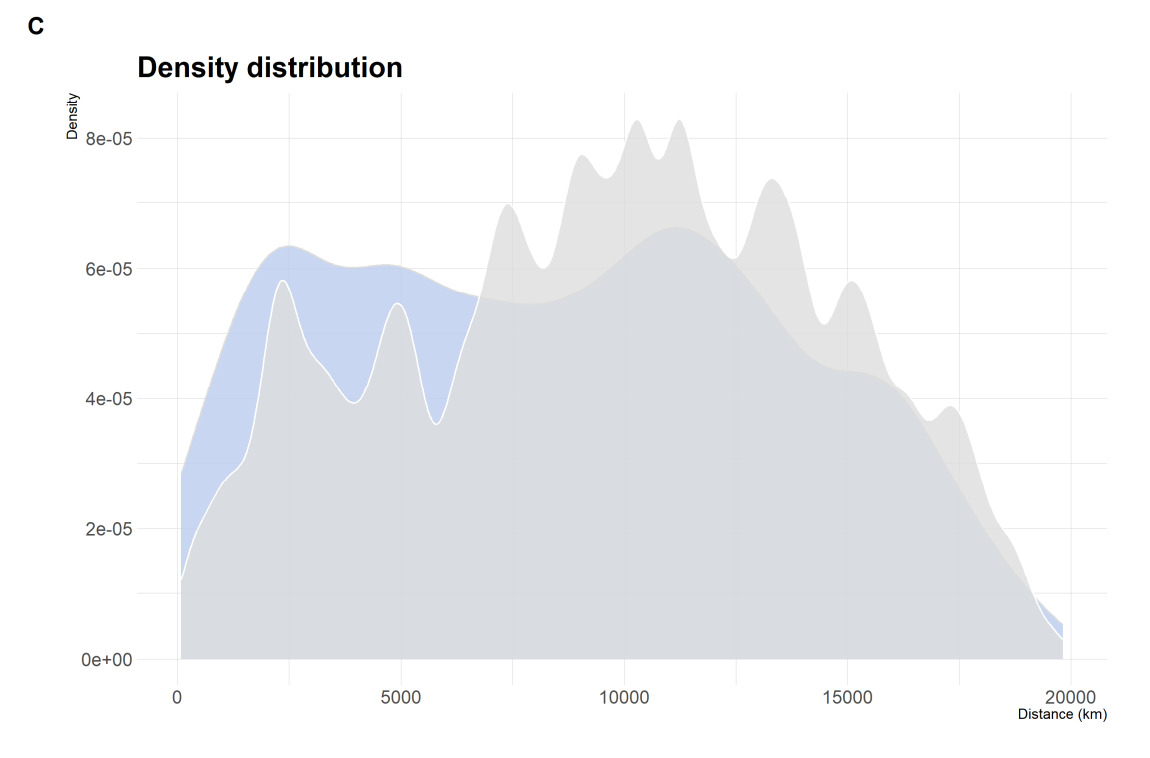
類似性を比較する際は二つの作品を比べますが、その際にそれぞれの作品が記録された国・地域間の距離を算出し、その距離を区間ごとに区切った度数分布表(ヒストグラム)も論文で示されています。ヒストグラムでは、コサイン距離が0.1未満(同一作品)だった作品群と0.1以上(非同一作品)だった作品群の二つに分けて図示されています(下図のA・B)。しかし、非同一作品同士の類似性比較の数の方が多く縦軸の度数の桁が合わないため、確率密度分布として縦軸を揃えて同一・非同一作品を比べています(下図のC)。そのCの図から、作品が記録された国・地域が近いほど同一作品の度数が多いため、近隣の異文化地域ほど類似するあやとり作品がより見つかる可能性が高いことを示唆している、と述べられています。
同一(A)・非同一(B)作品の地理的分布に関する分析のヒストグラム(論文の図4)
確率密度分布に変換した同一・非同一作品の地理的分布に関する分析のヒストグラム(論文の図4)
また作品が記録された地域は、上図ツリー構造の作品の背景色、つまり図中央の地図にある地域の色に対応しています。この作品が記録された地域の分布から、以下に述べる作品の起源についても考察されています。
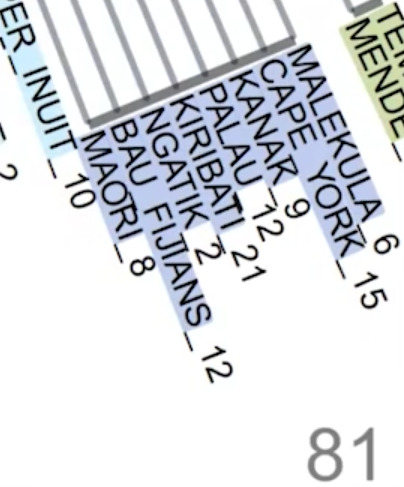
例えばツリー構造の最下部のうち、異なる文化地域で記録された、例えば「Ten men(10人の男)」(地域によっては「Mat」などとも呼ばれる)の作品を見ると、下図のように記録場所はどこもオセアニアの地域であることが分かります。
ツリー構造最下部のうち81番目の作品(10人の男)が記録された異文化地域
「10人の男」のあやとり作品
しかし、4段ばしごの作品を見ると、世界中の様々な国・地域で記録された作品であることが分かります。
ツリー構造最下部のうち1番目の作品(4段ばしご)が記録された異文化地域
この4段ばしご作品の複雑性は、変換した“数字の並び”のzipファイルサイズから3.77と算出され、826作品の中央値である2.11と比べると、比較的複雑な作品であると述べられています。そして作品の作り方の側面から考えると、4段ばしごは、多くの異文化地域間で同じ作り方が記録されていることにも触れられています。このように同じ作り方による複雑な作品が異なる地域で別々に生み出されたというのは考えにくく、また4段ばしごの網目状の特徴的な模様が、先史時代の史料に見られる模様に非常に似ていることなどから、4段ばしご作品はもっと昔まで遡った共通の起源がある可能性を示唆している、と考察されています。
以上、論文の紹介でした。こうしたあやとりに関する学術的な研究が行われたことを大変嬉しく思います。あやとりにまつわる研究を通じて、様々な議論や新たな研究の種が生まれ、更なるあやとりの発展に繋がることを期待しています。
今回の紹介にあたって、Kaaronen氏に複数回に渡り論文内容の確認をさせていただきました。ご対応いただいたこと、この場をお借りして改めて感謝申し上げます。
加藤直樹@ISFA
第20回今年も元気に「ゆびはまほうつかい」~善気山遊びの寺子屋報告~ 2024/08/10
恐ろしい!ことに「熱中症警戒アラート」は耳慣れてしまい、体温より高い38度、39度の数字は恐ろしい!気象予報の地図が赤と紫で埋め尽くされる一方で、日本の各地で突然の猛烈な雨で川が氾濫、土砂災害警戒発令、雷、ヒョウと被害が伴う異常気象の夏です。
今年の「遊びの寺子屋」は下記の日程で行われました。
南書院での【≪自由空間≫ゆったり、のんびり、おてらですごそう!】は「ゆびはまほうつかい」「お花の絵をかいてみよう」「本の森で遊ぼう」「お寺の森の生き物キルト」の企画は、誰でも自由に参加出来ました。
開催日時: 7月28日(日)・29日(月)10時~15時
講師: 青木萬里子(野口廣記念あやとり講習会指導員、国際あやとり協会会員)
参考資料: ①チラシ「あやとりは日本の遊びと思っていませんか?」 準備した物: 4本の手造りタペストリー
開催場所「法然院」の山門
「遊びの寺子屋」の入口
今年もお父さんと一緒に一番乗りをしたやる気満々の大和君は6年生。次々に上級を習得するあやとり名人です。指導員の加藤さんが都合で不参加となり、大和君に「今年は、あやとりを教えてあげる名人になってね。」と頼んでおきました。大和君の指導のもと「パンパンほうき」が上手にできた4歳の女の子はタペストリーの4段ばしごを指さして「これやりたい!」と。次も大和君の出番です。横にしゃがみ込みよく見えるように体制を整えて「ゆっくりでいいよ」と声をかける大和君。はしごの難所は最後の中指の動きです。大人でも難しい。要領が得られなくて何度も失敗している女の子に、「ここがちょっと難しいんだよ。でも、やれば出来るからがんばってね」と声をかける大和君。4歳の女の子の根気良さと大和君の無理強いしないやんわりとした関わりで、4段ばしごの完成!傍らにいたお母さんは2人に大きな拍手!大和君、教える名人!ご苦労様、ありがとう!
今年は大和君(左から2人目)にも指導してくださいました
4段ばしごを教える大和君(右)
例年参加して新たに挑戦されたり、教えたりと一役買ってくださっている北島さんは、落ち着いた雰囲気で優しく対応されます。傍らにいた女の子に声をかけて「ほうき」に挑戦。おばあちゃんも引き込まれて「コーヒーカップ→東京タワー」「富士山」が出来、嬉しそうでした。北島さん、ありがとうございました。
「次はこうやって・・・」と教える北島さん(右)
本を見ながら黙々と挑戦し満足げな様子の4年生の女の子に声をかけ、「流れ星」をした時に、「これは創作あやとりなんですよ。京都に住んでいるシシドさんという男の方が若い時に考えたあやとりなんです。」お母さんが「あやとりって自分で考えて作ったりするんですか?」「いろんな国にあるんですね。あやとりは奥が深いんですね」と感心されていました。あやとり万歳!
指導補助の青木さん。予習に余念がありませんでした。「パンパンほうき」「1段から6段までのはしご」「月にむらくも」「山の上のお月さん」「流れ星」「カモメ」「バトカ峡谷」など。「どうもバトカ峡谷は身近ではないな~はて?三角おにぎりが並んでいるように見えるな~」といって「おにぎり3兄弟」と見立てました。身近な食べ物に見立てるのはなかなか面白いではありませんか!男の子や女性とやる中で「おにぎりの中身は何が好きかな?」と会話も弾んでいました。
「富士山」を披露する青木さん(右から2人目)
観光客に人気王国・京都!真昼間のあっつあっつ京都は日本人は外出を控え気味なので、「ゆびはまほうつかい」と隣のコーナー「本の森であそぼう」はお昼寝状態。暑さにも負けずと琵琶湖疎水が流れる哲学の道をたどって名所散策してくる外人観光客は、銀閣寺、安楽寺、法然院にたどり着きます。善気山の緑の空気とおもむきのある法然院に誘われて身軽な格好で南書院に入ってきます。何時しか外人さんのための「遊びの寺子屋ゆびはまほうつかい」コーナーになっていました。
指導補助の青木幸久さんの出番です。あやとりへのお誘いを始め「富士山」「ほうき」「コーヒーカップ」などを一緒にしながら、完成型の説明、その場を盛り上げる会話など楽しんでいました。
28日、29日の2日間でフランス(2組6人)、イタリア(2組4人)、スペイン(2組4人)、アメリカ(2組4人)、トルコ・イスタンブール(1組4人)、中国2組(2人)、メキシコ(1組2人)でした。今までになく外国の方が多かったです。
これらの国々の人に、毛糸のひもを渡すと、まず、手首にひもを巻きつけ「二人あやとり」の準備を始める人が何人もいました。「田んぼ」「ダイヤ」「かえる」と次々取り合いました。子どものころにやったようです。やっぱり指が覚えているんですね。お互いに取り合って、懐かしがっている表情や指の入れる場所が「違う!違う!」と笑い合う光景が和やかでした。日本では一つ一つ名前がついていますが、それぞれの国ではどんな見立てをしているんでしょうね。
二人あやとりで楽しみました(その1)
二人あやとりで楽しみました(その2)
二人あやとりで楽しみました(その3)
勿論あやとりは初めての方もいました。短時間で出来上がる「富士山」「パンパンほうき」をやりました。手のひらに出来上がった時の感激は万国共通ですね。見ている側も笑顔いっぱいになります。あやとり万歳!
パンパンほうきの完成!
完成した感激は万国共通!
フランスの男性は「あやとりは子供の遊びだから、ぼくは大人だからやらないです!」と。そういえば日本には「女の子の遊びだから・・・・」という言葉を耳にすることがありますね。でも、世界各国で脈々と伝承されているあやとり。あやとり万歳!ですね。
参加して下さった皆様、ありがとうございます。
講師の記念撮影(左から青木萬里子、青木幸久)
法然院の梶田真章さん始め法然院の皆さん、森のセンターの久山ご夫妻始めスタッフの皆さん、いろいろありがとうございました。今年も元気で法然院遊びの寺子屋(あやとり参加16回目)で好きなあやとりをして過ごせたことに感謝いたします。ありがとうございました。
報告:青木萬里子@ISFA & 写真提供:青木幸久
第3回小規模あやとり検定報告 2024/07/22
去る7月13日(土)の午後に第3回小規模あやとり検定を実施致しました。
これに参加された方々は6月22日(土)に行われた第33回あやとり講習会・検定に申し込まれた方々でしたが、予想よりも多くの方のお申し込みがあって、限られた時間内に検定を終了させるために、臨時に設けられた検定でした。
都内在住で「あやとり教室指導員」を目指しておられる7名の方にこちらに移動して下さるようお願いしたところ、皆さん快く移動を受け入れてくださいました。
小規模検定は世話人宅で行われ、第1部は午後1時~3時で3名の方が参加され、休憩をはさんで、午後3時半~5時半までの第2部には5名の方が参加して下さいました。
あやとりの指導と検定は国際あやとり協会上級指導員の杉林武典先生と服部知明先生が引き受けてくださいました。
講習では、「白鳥」や「そりを引くトナカイ」など極めて難易度の高い極北圏のあやとりや、「テリハボクの花」「天の川」などオセアニアの超傑作あやとりが取り上げられ、皆さん熱心に習得されていました。
講習会のあとの検定も全員合格で、7名の方が「あやとり教室指導員」の資格を取得されました。検定では取り方だけでなく完成形の美しさも高く評価されるものがありました。
「天の川」
「テリハボクの花」
「ひきがえる」
「そりを引くトナカイ」
「白鳥」
親子で指導員の資格取得
「火山」
「山間の日の出」
「2匹の子鹿」
「キツネとクジラ」
「ねずみの顔」
「テリハボクの花」
「天の川」
「白鳥」
「お星さま」
「耳の大きな犬」
「ダンスハウスで踊る人々」
「白鳥」
最後のクラス
こうして「あやとり教室指導員」の資格を取得された方々は、次回の講習会で指導の実技を担当していただく事になっています。
講習会の参加者が年々増える一方でこうして素晴らしい指導員が次々と誕生していることは、日本におけるあやとりの将来が明るい事を思わされ、協力者の皆様方に深く感謝しております。
報告:野口廣記念あやとり講習会・検定 世話人 野口とも@ISFA & 写真提供:嶋津香
第33回野口廣記念あやとり講習会・検定報告 2024/06/30
2024年6月22日(土)の午後に東京代々木の国立オリンピック記念青少年総合センターで、第33回野口廣記念あやとり講習会と検定が行われました。
梅雨の時期で前日の東京はどしゃぶりの雨でしたが、当日はからりと晴れた初夏の1日となり、会場となったセンター棟4階の教室の窓からは緑の木々の葉が青空に映えて、心地よい空間を作り出してくれていました。
今回も関東一円だけでなく、関西方面や九州からの参加者もおられて、和やかな楽しい会となりました。
会の始めに世話人の野口ともの挨拶があり、続いて各指導員方たちによるあやとりの実演が行われました。最初は初級の青木萬里子先生が「お星さま」「流れ星」「七夕」等お星様シリーズを紹介して下さいました。続いて伊藤ひで先生が初心者のために「パンパンほうき」「おうむ」「はたおり」等動かして遊ぶあやとりを紹介して下さいました。初級の最後は吉井よし子先生がアフリカのあやとり「バトカ峡谷」「草ぶきの小屋」を紹介して下さいました。
中級は竹原庸光先生がアラスカのあやとり「かもめ」とカナダ先住民のあやとり「2匹の子鹿」を紹介して下さいました。続いて中級は吉田仁子先生がアメリカ・ナバホの「ナバホの蝶」と「いなずま」を紹介して下さいました。
上級はまず杉林武典先生が「はしご連続取り」を、服部知明先生がカナダ先住民のあやとり「白鳥」を実演して下さいました。
最後は前年に「あやとり教室指導員」の資格を取得した3人のお子さん達による実演で、藤本湊大君がナウルのあやとり「テリハボクの花」を、栗田亮佑君がパプアニューギニアのあやとり「天の川」を、金政奏佑君がツバルのあやとり「潮の満ち引き」の実演をして下さいました。あやとりはお子さんでも先生になれる素晴らしい遊びです。
先生方の実演の後は、参加者がそれぞれ自分の覚えたいあやとり名の書かれた席に移動して講習会が始まりました。
あやとりが完成すると思わず「できた~!!」という歓声が上がり、あちらこちらのテーブルで喜び合う姿が見られました。こうして時間の経つのも忘れてあやとりに夢中になっているうちに3時の閉会の時間になりました。今回初めて参加した或る大学生が「メチャ楽しかったです」と言って帰られたのが印象的でした。
売店では講習会のテキストとして使用されるあやとりの本の販売や、特注のあやとりひもの販売なども行われました。
午後3時半から、講習会と同会場であやとり検定が行われました。初級は3種出来たら合格です。中級は2種、上級は1種出来たら合格です。最近は1人で何回も受験する人が増えていますが、最高は1日に10回までとなっています。受験を終えて合格証を手にした時の喜びもまた格別のものがあるようです。合格証をかざしながら飛び跳ねて喜ぶお子さん達もいました。
今回は8名の方が初級2枚、中級3枚、上級5枚の合格証を集めて、「あやとり教室指導員」の資格を取得されました。
最後にスタッフ一同で記念写真の撮影を行いました。
「第33回野口廣記念あやとり講習会スタッフ」
講習会の翌日、指導員として参加した少年から以下のような手紙が寄せられました。
「先日のあやとり講習会にて、指導のお手伝いをさせていただきありがとうございました。僕自身も知らないあやとりがあったので、とても勉強になりました!そして、あやとりが好きな方々が沢山集まっていることに感動しました。実際に教えるのは、自分でとるのと違ってとても難しい事でしたが、とても楽しい時間でした。」
以上のように、あやとり講習会は教える方も教えられる方もとても楽しい時間となっています。ぜひ皆さんもこの楽しい、そして脳活性にもなる講習会に参加して共に楽しい時間を過ごしましょう。
報告:野口廣記念あやとり講習会・検定 世話人 野口とも@ISFA & 写真提供:嶋津香